[모각코] DP 3

1. 평범한 배낭

https://www.acmicpc.net/problem/12865
평범한 배낭 문제는 아주 대표적인 DP 문제인 01 배낭 문제이다.
한정된 무게를 담을 수 있는 가방에 각각 무게와 가치를 가진 물건을 가방에 담을 수 있는 최대 무게와 가치로 넣는 것이 목표이다.

테이블을 그려 가며 문제를 풀어보았다.
테스트 케이스 대로 테이블 표를 작성하면 아래와 같다. 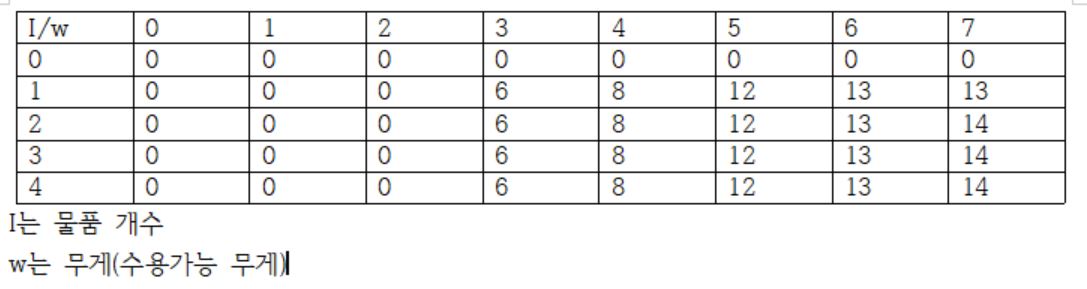![테이블](/img/DP3-1.JPG)

i = 1이고 w가 4일 때와 7일 때를 보자.
한 개의 물건을 넣는 데 4의 무게를 넣을 수 있다. 그렇다면 1,3 인 경우에 총 가치가 6이었고, 4의 무게를 가진 물건의 가치가 8이므로 둘을 비교했을 때 4의 무게를 가진 물건을 넣는 것이 맞다. 따라서 8이 된다.
7인 경우에는 이전에 넣었던 6일 때의 가치 13과 3+4의 가치 14 중 14가 크지만 여기서는 한 개의 물건만 넣을 수 있으므로 그대로 무게 6인 물건이 들어가 13이 된다.
하지만 바로 아래 2,7의 경우를 보자.
물건을 2개 넣을 수 있고 무게 한도는 7이다. 그렇다면 이전에 넣었던 6과 3+4의 가치 중 3+4의 가치가 더 크므로 6을 선택하지 않고 3+4를 선택하여 가치 합인 14가 되었다.

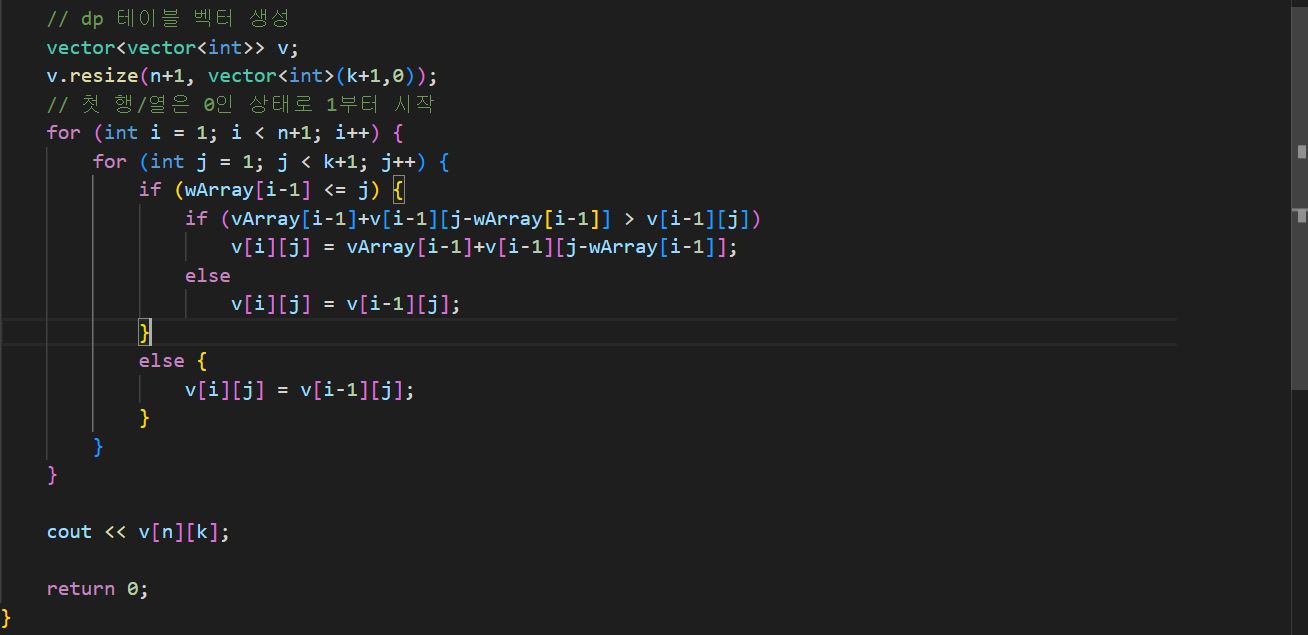
이렇게 테이블을 채우면서 식을 세울 수 있다.
넣으려는 물건의 무게가 무게 한도를 넘지 않는 경우에, 해당 물건의 가치+해당 물건을 넣을 공간 제외한 가치와 이전 값 중 큰 것을 선택해서 넣게 된다.
만약 물건의 무게 한도가 넘어간다면 이전 값을 그대로 사용해 테이블을 채울 수 있다.

따라서 어떤 식이 만들어지냐면
if 넣으려는 물건 무게 <= 총량
    if 넣으려는 물건 가치 + 해당 물건 제외한 공간 가치 > 이전 값
        넣으려는 물건 가치 + 해당 물건 제외 공간 가치
    else
        이전 값
else
    이전 값

이라는 식이 만들어진다.
이를 바탕으로 코드를 작성해보자.

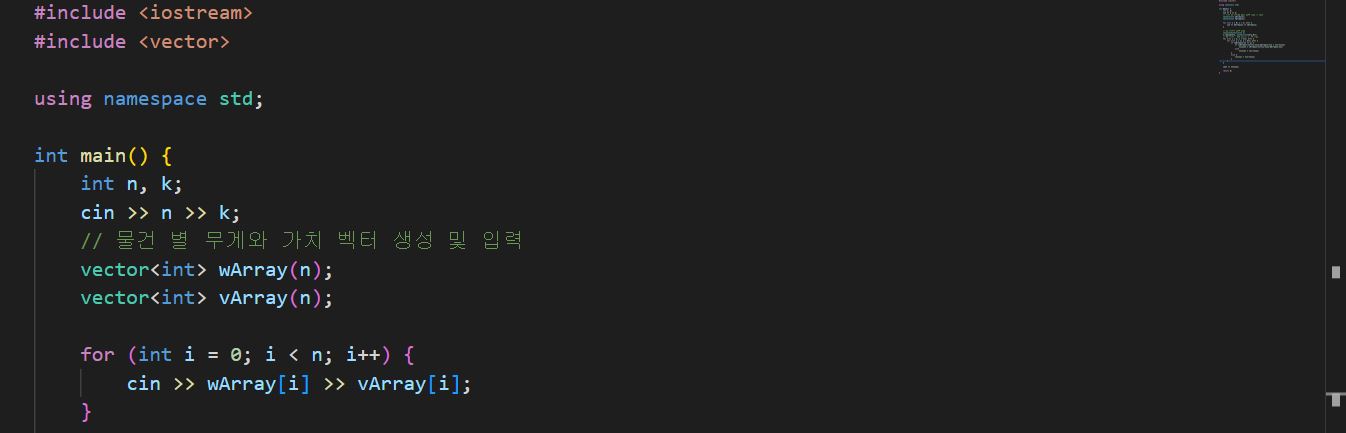
정답이 나왔음을 확인할 수 있다.

2. 마무리

정말 대표적인 DP 문제인 01 배낭 문제를 풀어 보았다.
아직까지 테이블을 만들 때 어떤 것을 기준으로 만들어야 할 지 감이 잘 오지 않아서
시간이 상당히 걸렸던 것 같다.
이전의 계산된 작은 문제에서의 최적 값을 이용해 그것으로부터 최적 값을 연속적으로 구해 나간다는 생각을 가지고 문제를 풀어보아야 할 듯 하다.
이번 문제에서도 이전 값 또는 넣을 무게와 그것을 제외한 계산된 값을 이용해 답을 찾아가는 문제였기 때문에 해당 개념을 문제에서 주어진 조건들 간의 관계성을 정립하는 데 사용하여 문제를 풀어봐야겠다.