[모각코] DP 4

1. 문제

https://www.acmicpc.net/problem/9251
오늘 풀어볼 문제는 LCS이다.
LCS란 최장 공통 부분 수열인데 두 문자열 사이에서 공통되는 가장 긴 문자열을 뜻한다.

어떻게 보면 간단할 지 모른다. 모든 인덱스를 참조하며 문자열을 만들고 비교하면 된다.
하지만 너무 오랜 시간이 걸리기 때문에 효율성이 떨어진다.

따라서 이 문제를 DP를 이용하여 풀어볼 것이다.

2. 풀이

기본적으로 각 문자열의 문자 하나하나를 비교해 나가야 하는 것은 맞다. 하지만 이를 DP를 이용해서 어떻게 풀어야 할까?

생각보다 간단한 아이디어이다. 한 문자열의 문자 하나를 다른 문자열 전체와 비교해 나가면서 같은 문자가 나왔다면 LCS길이에 +1을 해 주고,
다른 문자가 나왔다면 이전 문자에서의 LCS 길이를 가져오면 된다.

ABCD라는 문자열과 AFCD라는 문자열을 보자.
처음에 ABCD에서 A와 AFCD를 각각 비교한다.
A,A인 경우 LCS길이가 처음엔 0이므로 1을 더해 1이 된다. 그리고 A,F/A,C/A,D에서는 각각 이전 문자에서의 LCS, 즉 A,A에서의 1 또는 초기 값 중 큰 것을 선택해 가져온다.
따라서 모두 1이 된다.
B인 경우를 보자. B와 AFCD를 또 각각 비교한다.
B,A는 같지 않으므로 A,A 또는 B,초기값을 비교하여 A,A가 크므로 1을 가져와 1이 된다.
마찬가지로 B,F/B,C/B,D 모두 1이다.
다시 C를 보자. C,A/C,F는 같은 이유로 1이다.
C,C는 어떨까? 같은 문자이므로 이전 LCS값을 가져오는데, 이전 LCS값은 이전 문자에서 계산된 LCS 값이 아니라 대각선 방향 위쪽에서 가져온다. 즉 인덱스를 각각-1한 곳의 LCS값이다. 따라서 C,C는 B,F에서의 LCS값에 1을 더한 값을 LCS로 갖는다.
왜 1을 더하냐면 C라는 공통 부분이 발생했기 때문에 LCS가 1이 늘어나는 것이다.

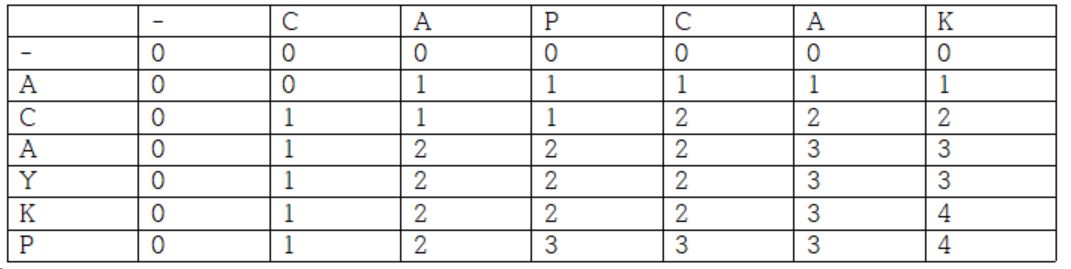
이런 아이디어를 가지고 테스트 케이스에 주어진 문자열로 LCS 표를 만들어 보자.

예제 출력과 같이 LCS 길이가 4인 것을 확인할 수 있다.

3. 해결

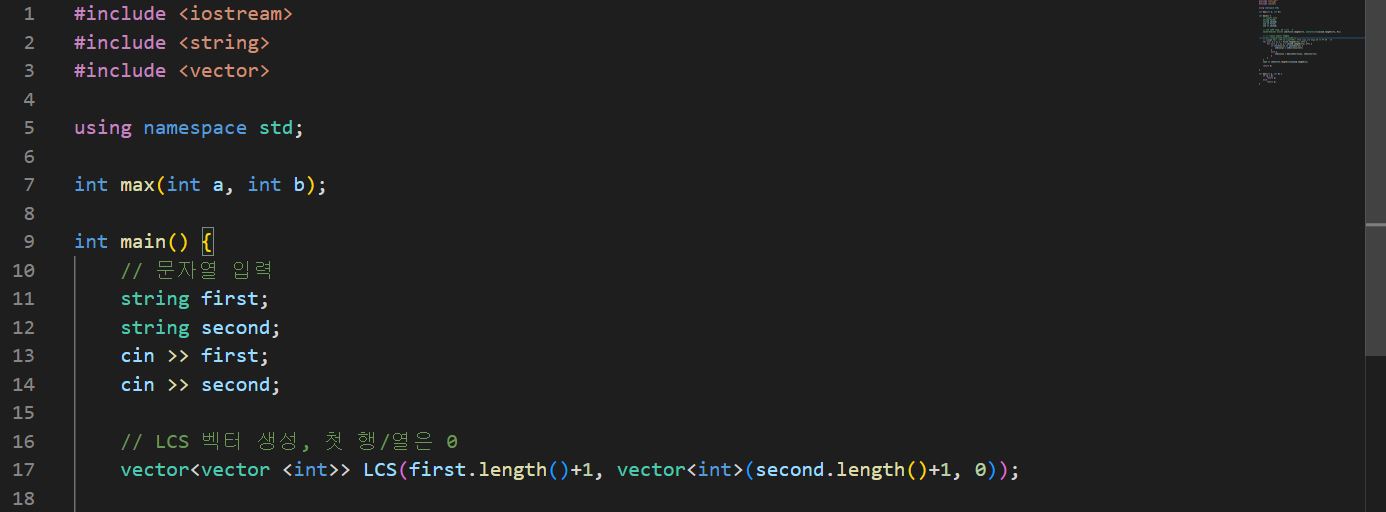
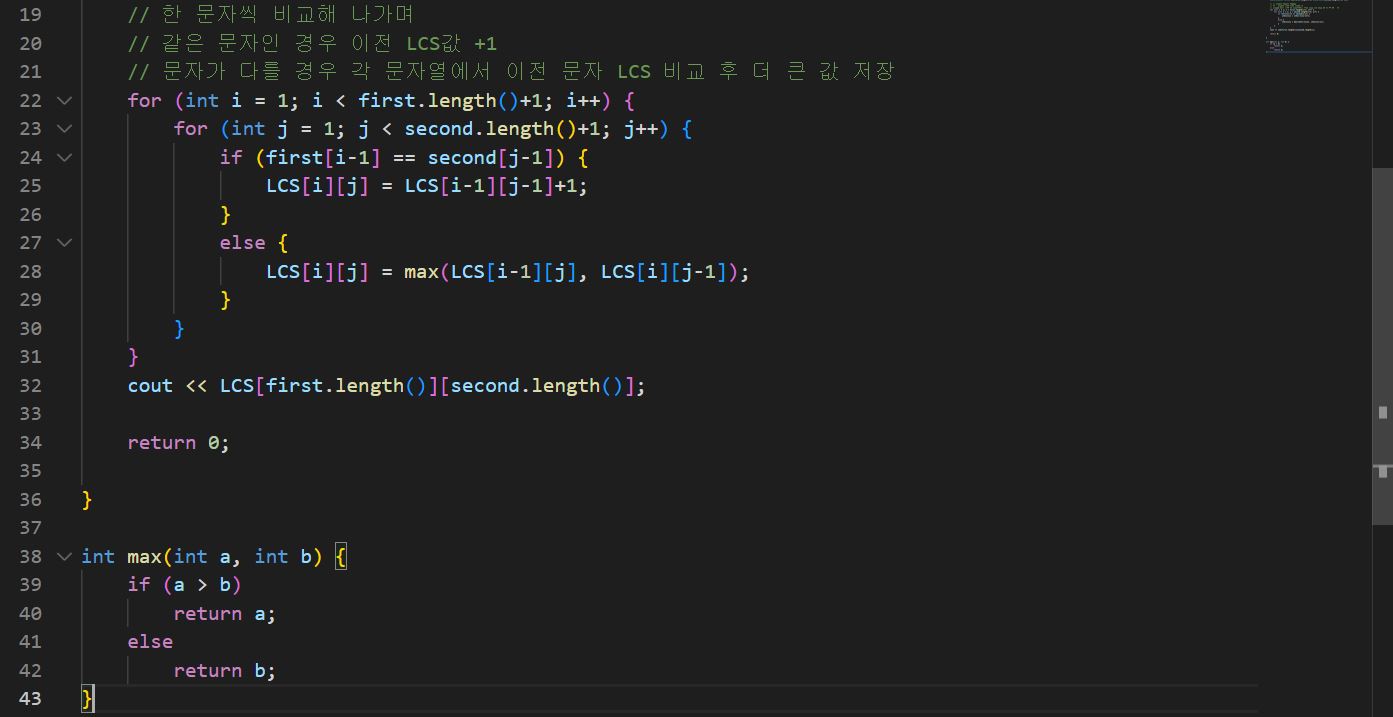
표도 그려봤으니 본격적으로 소스 코드를 작성해 보자.

정답으로 해결된 것을 볼 수 있다.

4. 마무리

문제를 몇 개 풀어나가다 보니 점점 DP를 활용하여 풀 수 있는 문제들의 특징이 보이기 시작하는 것 같다.
개념 공부를 할 때 부분의 최적 결과가 전체 문제의 최적 결과가 된다는 것과 작은 문제로 반복하여 해결한다는 말이 두루뭉술하게 이해가 됐었는데 지금은 무슨 의미인지 이해가 되고 있다.

이번 문제도 앞 부분에서 공통된 문자열을 선택했던 것이 뒷 부분을 풀어나가면서도 유지되며 그 문자열에 추가되는 방식이다.
DP로 문제를 풀 때는 확실히 내가 작은 문제들에서 규칙을 찾고 결과를 도출한 것들을 큰 문제에 어떻게 이용할 수 있을까를 고민하는 것이 중요하다고 생각된다.
여전히 규칙을 찾고 큰 문제에 어떻게 적용할지에 대해서는 감이 잘 오지 않지만 다양한 문제를 더 풀어보며 이해하기 위한 기초적인 힘은 길러진 것 같다.